Simulation of confidence ratings and RTs in leaky competing accumulator model

Simulates the decision responses, reaction times and state of the loosing accumulator together with a confidence measure in the leaky competing accumulator model. Optionally, there is a post-decisional accumulation period, where the processes continues.

Usage

rLCA(n, mu1, mu2, th1, th2, k = 0, beta = 0, SPV = 0, tau = 0,
  wx = 1, wrt = 0, wint = 0, t0 = 0, st0 = 0, pi = 0, sig = 1,
  time_scaled = TRUE, simult_conf = FALSE, delta = 0.01, maxrt = 15)

Arguments

n: integer. number of samples.
mu1: mean momentary evidence for alternative 1
mu2: mean momentary evidence for alternative 2
th1: decision threshold for alternative 1
th2: decision threshold for alternative 2
k: leakage (default: 0)
beta: inhibition (default: 0)
SPV: variation in starting points (default: 0)
tau: fixed post decisional accumulation period (default: 0)
wx: weight on balance of evidence in confidence measure (default: 1)
wrt: weight on RT in confidence measure (default: 0)
wint: weight on interaction of evidence and RT in confidence measure (default: 0)
t0: minimal non-decision time (default: 0)
st0: range of uniform distribution of non-decision time (default: 0)
pi: factor for input dependent noise of infinitesimal variance of processes (default: 0)
sig: input independent component of infinitesimal variance of processes (default: 1)
time_scaled: logical. Whether a time_scaled transformation for the confidence measure should be used.
simult_conf: logical. Whether in the experiment confidence was reported simultaneously with the decision. If that is the case decision and confidence judgment are assumed to have happened subsequent before the response. Therefore tau is included in the response time. If the decision was reported before the confidence report, simul_conf should be FALSE.
delta: numerical. Size of steps for the discretized simulation (see details).
maxrt: numerical. Maximum reaction time to be simulated (see details). Default: 15.

Value

Returns a data.frame with three columns and n rows. Column names are rt (response time), response (1 or 2, indicating which accumulator hit its boundary first), and conf (the value of the confidence measure; not discretized!).

Details

The simulation is done by simulating discretized steps until one process reaches the boundary with an update rule: $$\delta X_i(t) = \max (0, X_i(t) + \delta_t ((k-1)X_i(t)-\beta X_{j=i} (t) + \mu_i + \varepsilon_i (t)),$$ with $\varepsilon_i(t) \sim N(0, (\pi \mu_i)^2 + \sigma^2 )$. If no boundary is met within the maximum time, response is set to 0. After the decision, the accumulation continues for a time period (tau), until the final state is used for the computation of confidence.

Author

Sebastian Hellmann.

Examples

# minimal arguments
simus<- rLCA(n=20, mu1=1, mu2=-0.5, th1=1, th2=0.8)
head(simus)
#>     rt response        xl        x1        x2       conf
#> 1 0.33        1 0.4137317 1.0565648 0.4137317 -0.4137317
#> 2 0.21        1 0.0000000 1.0309454 0.0000000  0.0000000
#> 3 0.65        2 0.5460133 0.5460133 0.8193920 -0.5460133
#> 4 0.46        1 0.2443092 1.0223498 0.2443092 -0.2443092
#> 5 0.50        2 0.5446682 0.5446682 0.9163853 -0.5446682
#> 6 0.32        1 0.1821128 1.0370121 0.1821128 -0.1821128

# specifying all relevant parameters
simus <- rLCA(n=1000, mu1 = 2.5, mu2=1, th1=1.5, th2=1.6,
               k=0.1, beta=0.1, SPV=0.2, tau=0.1,
               wx=0.8, wrt=0.2, wint=0, t0=0.2, st0=0.1,
               pi=0.2, sig=1)
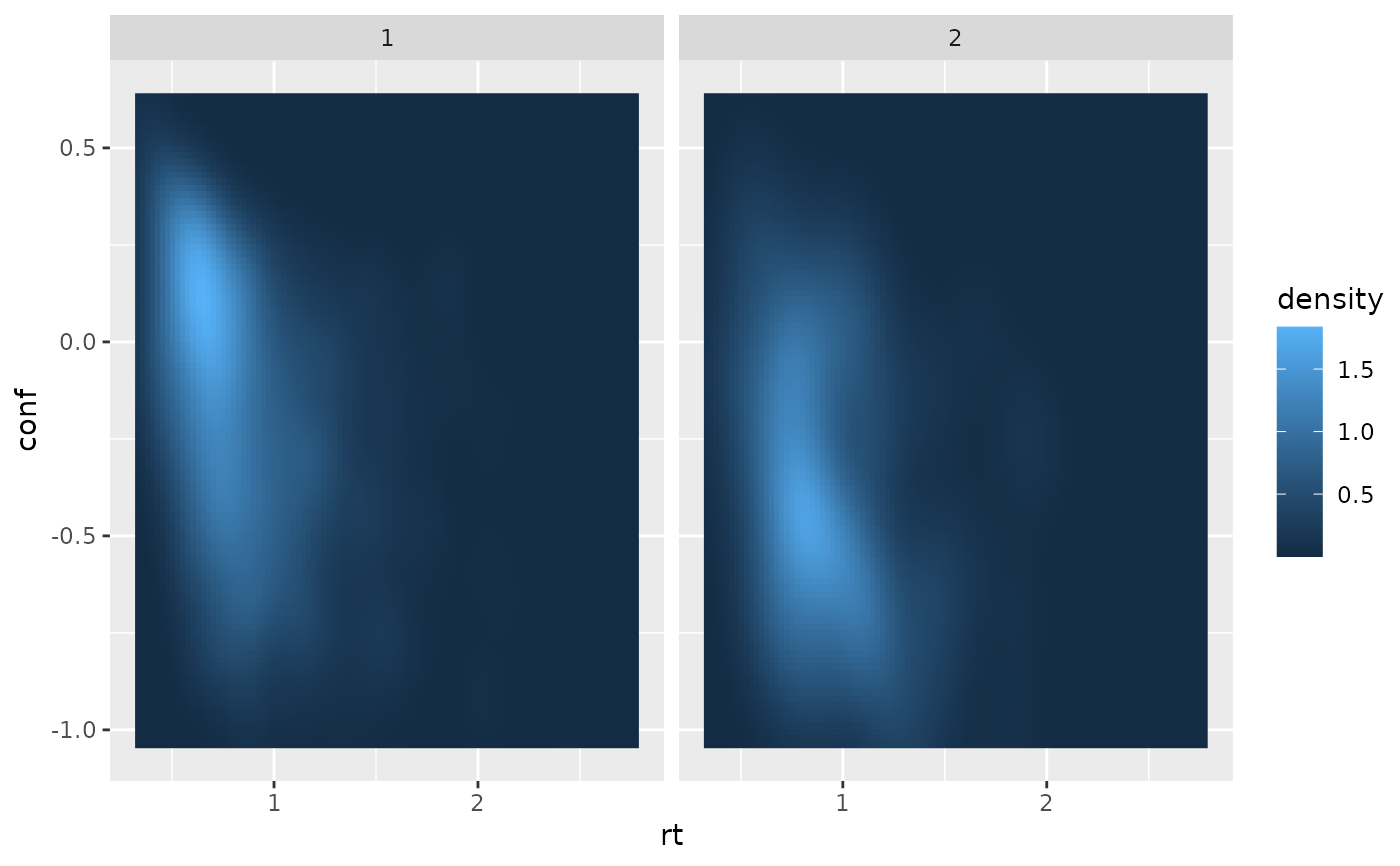
if (requireNamespace("ggplot2", quietly = TRUE)) {
  require(ggplot2)
  ggplot(simus, aes(x=rt, y=conf))+
    stat_density_2d(aes(fill = after_stat(density)), geom = "raster", contour = FALSE) +
    facet_wrap(~response)
}

boxplot(conf~response, data=simus)